Wien’s Law
What is it?
Wien’s Law tells us where (meaning at what wavelength) the star's brightness is at a maximum. See the picture below –the red dot under the word “visible” is the peak for the 6000 K object. In other words, Wien's law tells us what color the object is brightest at. As the surface temperature rises, this peak intensity (brightness) shifts toward the bluer end of the spectrum. As the surface temperature decreases, the peak intensity/brightness will shift more towards the redder end of the spectrum as shown by the red dot in the picture below.
Official Definition: Wien’s Law (also called Wien’s Displacement Law) is defined as so: For a blackbody (or star), the wavelength of maximum emission of any body is inversely proportional to its absolute temperature (measured in Kelvin). As a result, as the temperature rises, the maximum (peak) of the radiant energy shifts toward the shorter wavelength (higher frequency and energy) end of the spectrum (bluer). This is what the equation looks like:
Peak Intensity (Max Brightness) occurs at this Wavelength l(max) (in meters) =
0.0029meters ∙K
T (in Kelvin)
The wavelength lambda(max) is where the intensity is a maximum; T is the star’s average surface temperature measured in Kelvin; and the 0.0029 meters x Kelvin is known as Wien’s constant:.
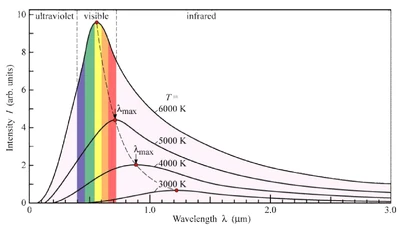
Image Credit: http://chriscolose.wordpress.com/2010/02/18/greenhouse-effect-revisited/
The curves above are Planck curves for objects at different temperatures. Planck's law tells us how intense the thermal emission is at each wavelength. The peak of this Planck curve (the red dot) is what Wien’s Law tells us.
Wien's Law tells us that objects of different temperature emit spectra that peak at different wavelengths.
· Hotter objects emit most of their radiation at shorter wavelengths; hence they will appear to be bluer.
· Cooler objects emit most of their radiation at longer wavelengths; hence they will appear to be redder.
Remember, at any wavelength, a hotter object radiates more energy (is more luminous or brighter) at all wavelengths than a cooler one.
Example: What wavelength (in nanometers) is the peak intensity of the light coming from a star whose surface temperature is 11,000 Kelvin? (Note: This is about twice the temperature of our Sun’s surface.)
Let’s plug the numbers into our Wien’s Law equation: Wavelength λ(max) in meters =
0.0029meters ∙K
11,000 K
We divide, the Kelvin cancels out and we are left with: λ(max) = 0.000000263 (which in scientific notation is 2.63 x 10-7)meters. Since we know that there are 1,000,000,000 (one billion) nanometers in a meter, we simply multiply our answer
by one billion to convert it from meters to nanometers: 0.000000263 x 1,000,000,000 = 263 nm.
What color would we see with our eyes? Would we even be able to see it?
The answer to both of these questions is that a wavelength of 263 nanometers is in the ultraviolet (UV) part of the electromagnetic spectrum. Our eyes can’t really see any wavelengths smaller than about 380 nanometers so we wouldn’t even be able to see this star’s peak light.
You can find more examples at: http://mintaka.sdsu.edu/faculty/wfw/CLASSES/ASTROBIO/LECTURES/wien_law.pdf